Calculate the Vertices Coordinates of an Icosahedron

Try this interactive 3D model of an icosahedron before moving onto the rest of this article. You can find the download link at the end of this page.

An icosahedron is a polyhedron with 20 faces. The regular icosahedron has all its 20 faces made from equilateral triangles. The well-defined polyhedron can be mathematically solved for the vertices’ coordinates. First of all, let’s get ourselves familiar with the icosahedron 3D structure. The 20-face polyhedron can be divided into 3 sections: the 5-face top, the 10-face middle and the 5-face bottom. Since this is a regular icosahedron, the distance between all the vertices to the center are the same. So, all the vertices coincide with a sphere. Let’s assume the radius of this “virtual” sphere is 1.

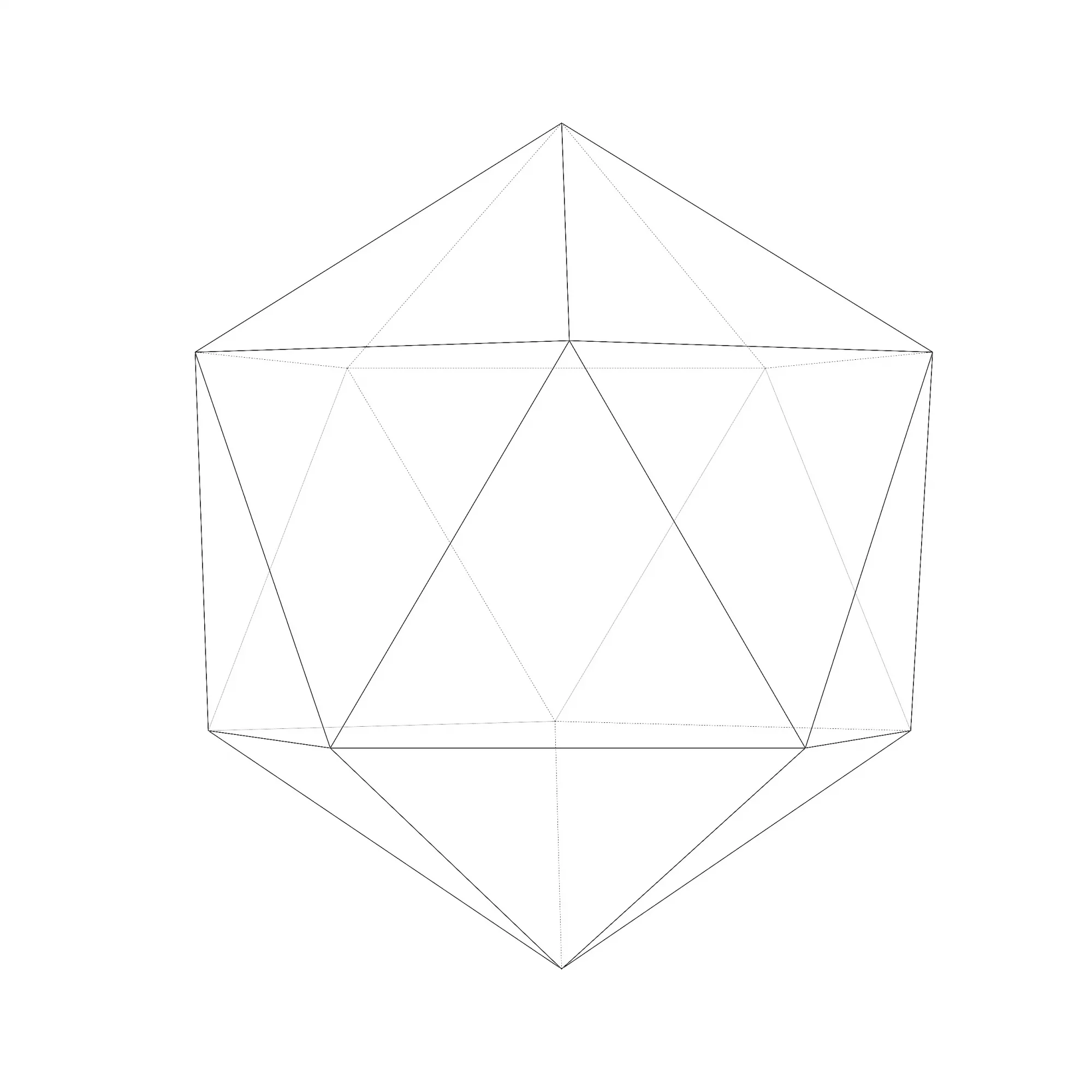
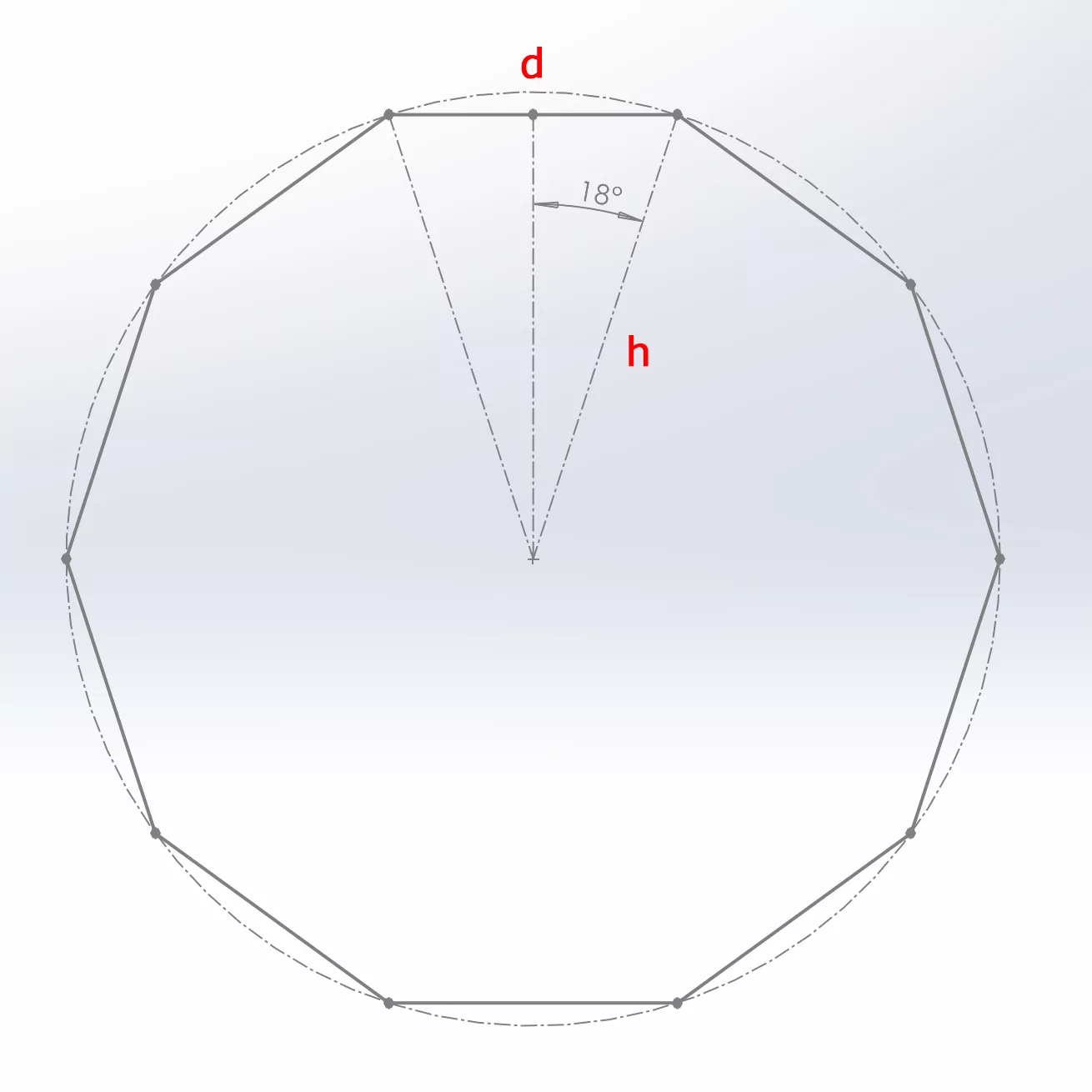
If we draw midlines on each of the 10 middle triangular faces as below, we will get a regular decagon, as shown on the right side of the gallery below. We are obviously interested in d, because d is the midline, or in other words, half of the side of each face. It’s easy to learn that d = 2 * h * sin18 ①, the so problem is to compute the h. Please note h is shorter than the radius of 1.

So, what is h? If we take a look at the figure below, h is actually the heigh of the triangle highlighted in red. Since the distance between the center and the vertex is 1, we have h = 1 * cos a ②. Combine this with the equation ① above, we get d = 2 * cos a * sin 18 ③. From the figure below, we can also find the relationship between the radius and the side of each triangular face. Let’s denote s as the side, so we have ½ s = sin a ④. Given d is the midline of the triangle, we have d = ½ s ⑤. Combine ③, ④ and ⑤, we get sin a = 2 * cos a * sin 18 ⑥.

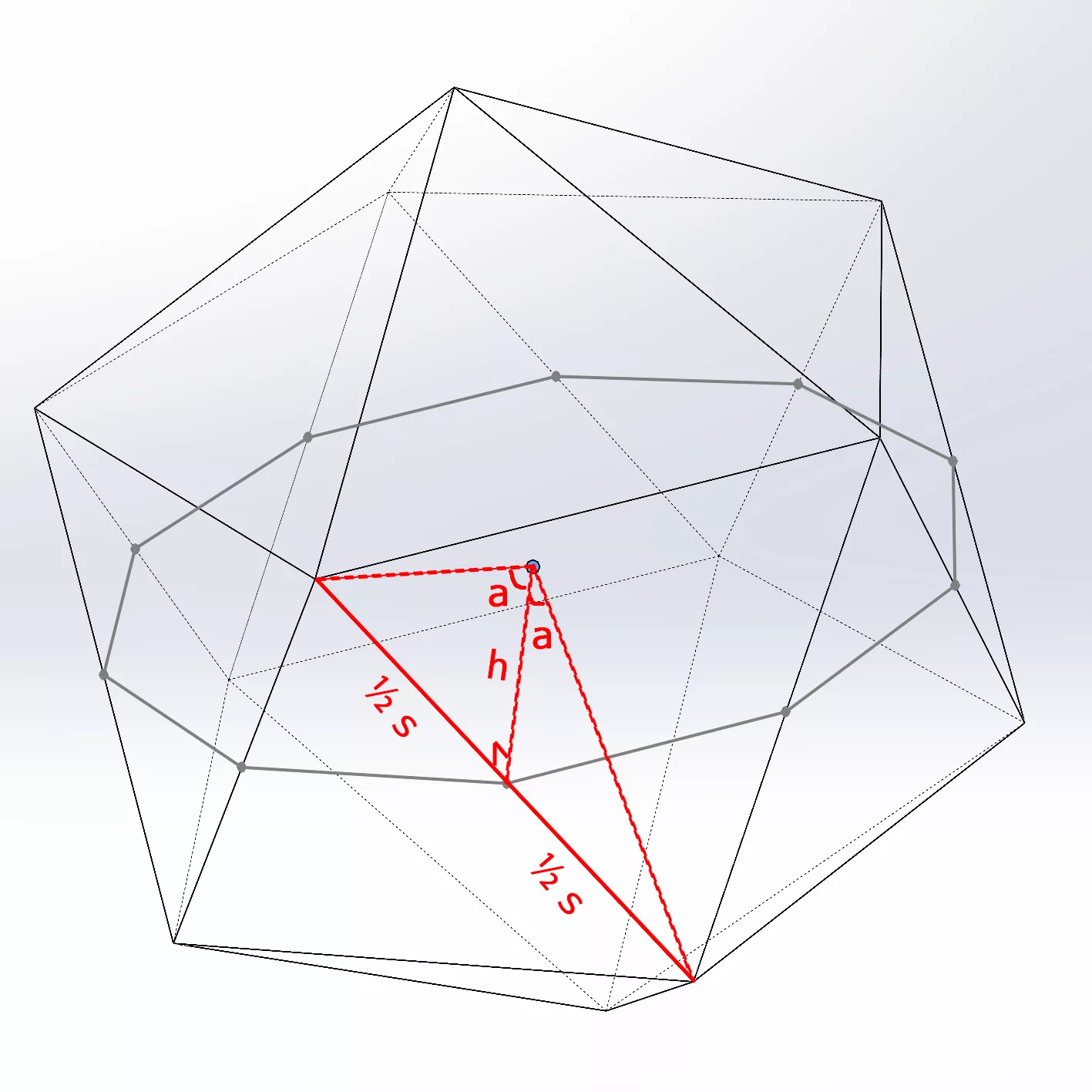
Equation ⑥ can be transformed into tg a = 2 * sin 18, we can compute a = arctg 2 * sin 18. Solving the a, we get the angle between each two adjacent vertices (∡ 2a) is 63.4349°, and the side of each face (s) is 1.051461.

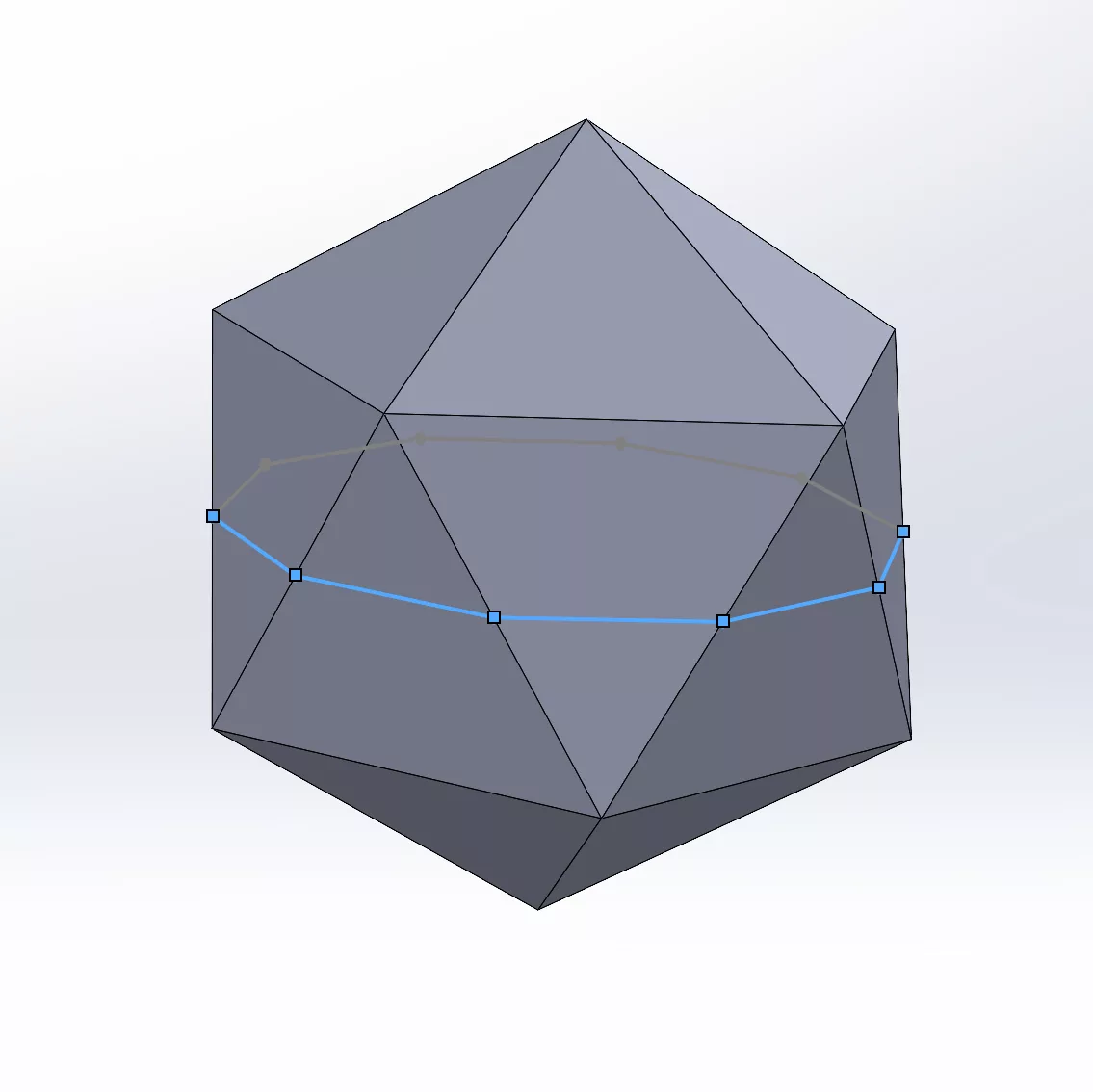
Next, we will calculate the coordinates for all 10 vertices. We define the XYZ axes as shown in the figure below:

• The X (left and right) axis goes through the center point and intersects line FG and line DI at their mid-points.
• The Y (up and down) axis goes vertically through the top and bottom pivot as well as the center point.
• The Z (front and back) axis goes through the center point and the mid-point of the △BGH and △CID.

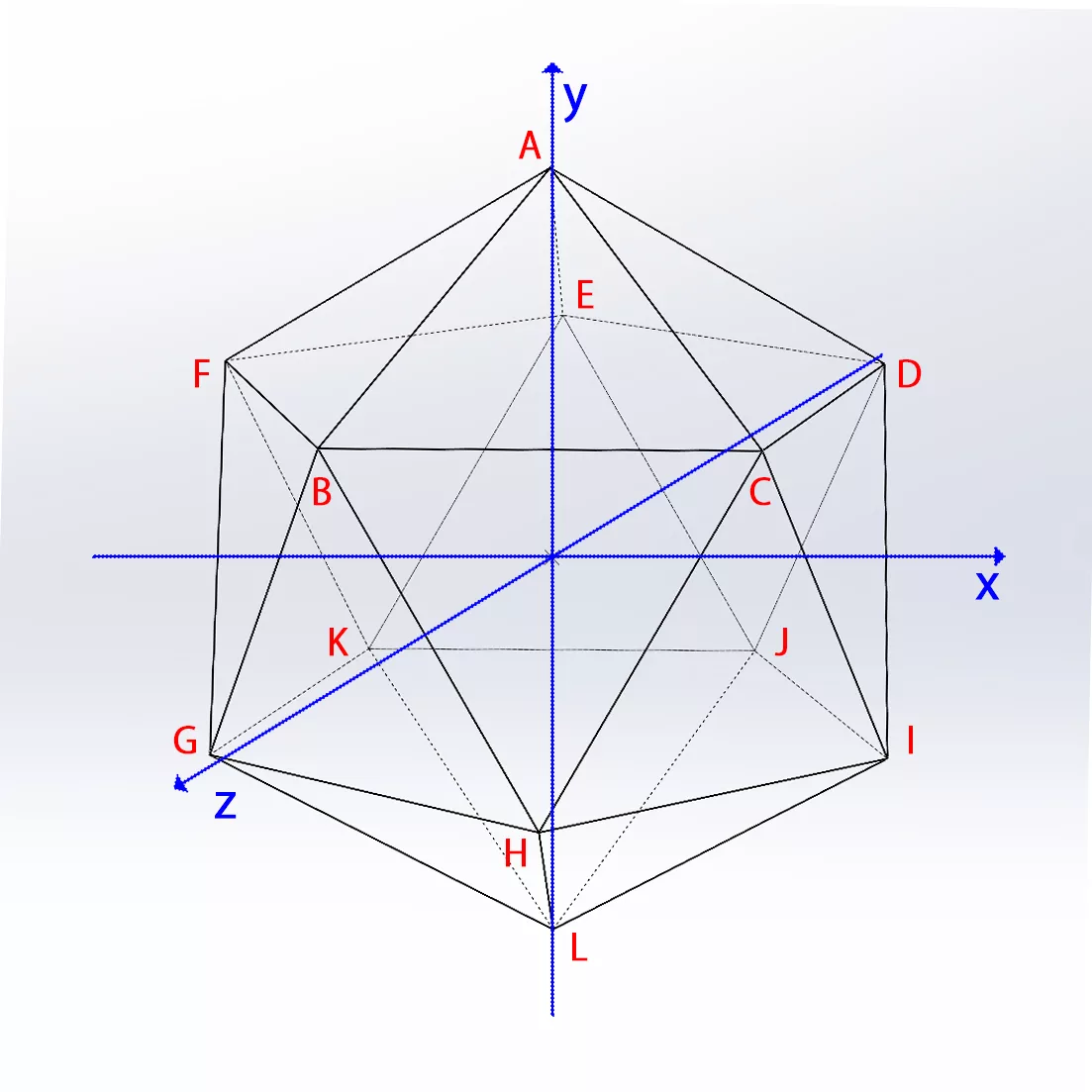
Based on the above definition and radius = 1, We have A (0, 1, 0). Since the B is on the plane YZ, so its X coordinate is 0, and

• Y = 1 * cos 2a = cos( 2 * arctg( 2 * sin (18) ) ) ≈ 0.44721
• Z = 1 * sin 2a = sin( 2 * arctg( 2 * sin (18) ) ) ≈ 0.89443

So, we get B (0, 0.44721, 0.89443). Since BCDEF forms a regular pentagon. We can easily compute the coordinates for C, D, E and F by rotating B along the Z axis by 72°, 144°, 216° and 288°. Similar approaches can be applied to calculate the coordinates for the lower half of the icosahedron. Below is a complete list of all 12 vertices’ coordinates:

A 0 1 0
B 0 0.4472135955 0.894427191
C 0.8506508084 0.4472135955 0.2763932023
D 0.5257311121 0.4472135955 -0.7236067977
E -0.5257311121 0.4472135955 -0.7236067977
F -0.8506508084 0.4472135955 0.2763932023
G -0.8506508084 -0.4472135955 -0.2763932023
H -0.5257311121 -0.4472135955 0.7236067977
I 0.5257311121 -0.4472135955 0.7236067977
J 0.8506508084 -0.4472135955 -0.2763932023
K 0 -0.4472135955 -0.894427191
L 0 -1 0

Download the 3D model of the regular icosahedron in OBJ format.